3명의 여자 친구를 동시에 사귀고 있는 플레이보이가 있다. 3명의 여자 친구를 원활히(?) 동시에 사귀기 위한 플레이보이의 전략은 각자의 여자 친구들의 집에서는 데이트를 하지만, 자신의 집에는 여자 친구를 데리고 오지 않는 것이다. 그것이 안전하다고 생각했다. 3명의 여자 친구(A, B, C)가 살고 있는 지역의 도로는 다음과 같다.

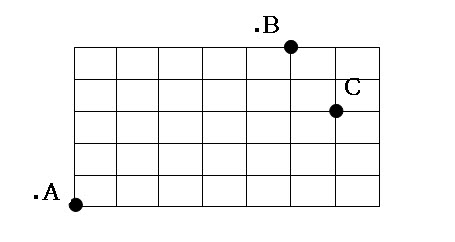
어느 날 플레이보이는 이사를 하기로 했다. 이 플레이보이가 고려하는 것은 “어느 지점으로 이사를 해야 최소의 노력으로 3명의 여자친구 A, B, C의 집을 왔다 갔다 할 수 있을까?”이다. 플레이보이는 3명의 여자 친구 집에 왔다 갔다 하는 자신의 일을 최소화 하기 위해서 다음과 같이 이 문제를 생각했다.

바둑 판과 같은 길을 따라, A, B, C가 위 그림과 같이 있을 때, PA + PB + PC의 길이가 최소가 되는 점 P의 위치는? (물론, 그 P 점의 위치로 플레이보이는 이사를 갈 것이다.)

어려운 문제를 잘 해결하는 사람은 복잡한 문제를 복잡한 상황에서 한번에 쉽게 해결하는 것이 아니다. 그들의 주된 방법은 복잡한 문제를 단순한 형태로 바꿔서 쉬운 것부터 하나하나 해결한다는 것이다. 이 문제는 복잡한 문제다. 이것을 쉬운 형태로 바꿔보자. 이런 경우를 생각해보자.

여자 친구들이 다음과 같이 같은 라인의 길을 따라 살고 있다. 이 플레이보이는 어디쯤 이사를 해야 각각의 여자 친구의 집에 왔다 갔다 하는 노력이 최소가 될까?

이 문제를 수식으로 다시 말하면 다음과 같다. 수직선 위에 A, B, C가 위 그림과 같이 있을 때, PA + PB + PC의 길이가 최소가 되는 점 P의 위치는?

이 문제는 경우를 잘 나눠서 생각해보면, B점을 P로 삼을 때 PA + PB + PC의 값이 최소가 된다. 이렇게 생각해보자. P점은 A와 C 사이에 있다. 따라서 P가 A와 B 사이에 있는 경우와 P가 B와 C사이에 있는 경우로 나눠서 생각할 수 있다.

- P가 A와 B 사이에 있는 경우: P가 A와 B 사이에 있으므로 PA + PB = AB로 일정하다. 따라서 A와 B 사이에 있는 점 중에서 C와의 거리가 최소인 점을 P로 잡으면 된다. 즉, P를 점 B로 잡으면 된다.

- P가 B와 C 사이에 있는 경우: P가 B와 C 사이에 있으므로 PB + PC = BC로 일정하다. 따라서 B와 C 사이에 있는 점 중에서 A와의 거리가 최소인 점을 P로 잡으면 된다. 즉, P를 점 B로 잡으면 된다. 즉, P가 A와 B 사이에 있는 경우와 P가 B와 C사이에 있는 경우 모두 점 P를 점 B로 잡으면 되므로 P = B 이다.

이제 얻어진 결과를 사용하여 앞의 플레이보이의 고민을 해결해 보자. 플레이보이가 움직이는 길은 바둑 판처럼 생겨서 상하좌우로만 움직일 수 있다. 움직이는 방향은 수평과 수직의 2방향으로 나눌 수 있다. 따라서, 수평 방향으로의 최소 점과 수직 방향으로의 최소 점을 좌표로 잡는 점이 P점이다. 그림과 같다.

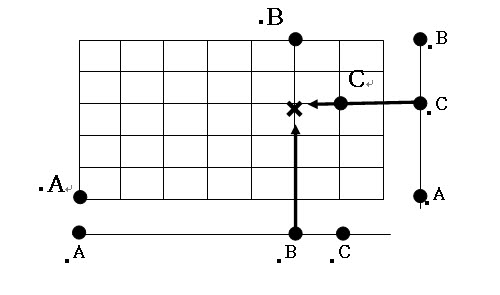
어렵고 복잡한 문제를 단순화시켜서 쉬운 문제로 바꿔서 해결하는 것이 분석이다. 어려운 문제를 잘 해결하는 사람들이 있다. 그러나 나에게 어려운 문제는 다른 사람에게도 어렵다. 어려운 문제를 잘 해결하는 사람은 복잡함을 잘 다루는 사람이 아니라, 복잡한 것을 쉬운 형태로 잘 나누는 사람이다. 그들의 진짜 힘은 복잡함을 잘 다루는 것이 아닌, 복잡함을 단순함으로 잘 분해하는 능력에 있다.

지금 우리 앞에 있는 골치 아프고 복잡한 문제도 이해하고 조작할 수 있는 작은 부분으로 나눠서 생각해보자. 하나의 어려운 문제를 풀려고 하지 말고, 어려운 문제를 여러 개의 쉬운 문제로 바꿔서 해결해보자. 그것이 바로 분석이다.  

글. 박종하 박종하창의력연구소 대표