문제 2개를 풀어보자. 첫 번째 문제를 소개하면 다음과 같다.

[문제 1] 물과 포도주

똑같은 크기의 두 컵이 있다. 하나의 컵에는 포도주가 있고 다른 컵에는 물이 있다. 포도주를 한 숟가락 떠서 물이 담긴 컵에 넣어 잘 휘저은 다음, 이번에는 반대로 물을 한 숟가락 떠서 포도주가 담긴 컵에 넣는다. 동일한 과정을 한번 더 되풀이 한다. 포도주가 담긴 컵 안에 있는 물의 양과 물이 담긴 컵 속의 포도주 양을 비교하면 어느 쪽이 더 많을까?

이 문제는 풀기 위해 제시한 문제라기보다는 같이 생각하기 위해 제시한 문제다. 하지만, 이런 문제 풀이를 즐기는 사람은 잠시 문제를 생각해보라.

이 문제의 정답은 포도주가 담긴 컵의 물의 양과 물이 담긴 컵 속의 포도주의 양의 비율은 같다는 것이다. 이 문제를 풀기 위해서 일일이 분량이나 농도를 계산하려고 한다면, 문제는 매우 어려워진다. 이 문제는 순차적으로 생각하는 것보다는 최종단계에서부터 거꾸로 생각하는 것이 효과적이다.

물컵에서 한 숟가락을 떠서 포도주 컵에 넣고, 또 포도주 컵에서 한 숟가락을 떠서 물컵에 넣었기 때문에, 이런 과정을 반복하여도 두 컵 안에 있는 액체의 양은 똑같다. 물 컵 속에 이전에 없던 포도주가 들어와 있다면 그 양만큼의 물이 포도주 컵으로 간 것이다. 그래서 결과적으로 물 속의 포도주 양과 포도주 속의 물의 양은 같은 것이다. 

이 문제는 순차적으로만 생각하면 해답을 제대로 생각할 수 없다. 생각의 순서를 거꾸로 뒤집어서 물과 포도주가 모두 섞인 후의 최종적인 상황에서부터 생각하면 이해할 수 있다.

일반적으로 관점을 전환하고 시각을 바꾸는 가장 쉬운 방법이 거꾸로 생각하는 거다. 일이 일어나는 순서대로 순차적으로 생각하는 것이 아니라, 최종적인 상황에서부터 거꾸로 생각을 되짚어보는 거다. 또 하나의 문제를 소개한다.

[문제 2] 토너먼트 경기

100명이 참가한 테니스 경기에서 토너먼트 방식으로 우승자를 결정한다. 토너먼트 방식으로 우승자가 나올 때까지 모두 총 몇 경기가 벌어질까?

계산이 되나? 아마 당신은 계산을 하기 위해서 머리 속에 대진표를 생각했을 거다. 100명에서 출발하여 단계를 거처 올라가는 대진표를 머리 속에 넣고 총 경기 수를 계산해보자. 

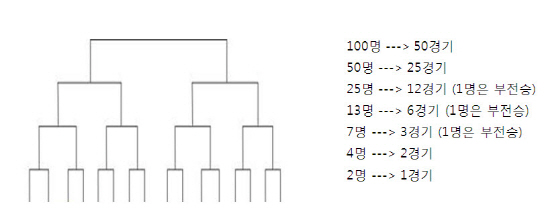
총 경기 수는 99경기다. (99 = 50 + 25 + 12 + 6 + 3 + 2 + 1)

이 문제를 쉽게 푸는 방법을 소개한다. 당신의 머리 속에 그려진 대진표를 지워라. 그리고, 우승자가 아닌 패자에게 문제의 초점을 전환시켜보는 거다. 토너먼트 방식이란 한 시합마다 한 사람씩 탈락된다. 그리고 우승자는 단 한 명 나온다. 따라서 100명 중 1명을 제외한 99명은 모두 한 경기씩 지고야 말았을 것이다. 즉 그들이 벌인 총 경기 수는 99번인 것이다. 이 상황을 정리해보면 이렇다.

참여자 100명 = 우승자 1명 + 패자 99명

우리가 우승자 1명에 초점을 맞추면, 우리는 머리 속에 대진표를 그리게 된다. 대진표를 단계단계 올라가면 최종단계에 우승자가 1명 남는다. 하지만, 초점을 우승자 1명에서 패자 99명으로 바꿔보는 거다. 우승자를 머리 속에서 지우고 대진표를 머리 속에서 지워야 한다. 그리고 생각의 출발점을 탈락자 99명에 맞춰보는 거다.

그들은 모두 딱 한번씩만 경기에서 지고 탈락한 사람들이다. 따라서, 99명의 탈락자가 나오기 위해서는 99번의 경기가 필요하다. 이렇게 패자의 관점으로 보면, 587명이 참여하는 테니스 경기에서 토너먼트 방식으로 우승자가 나오기까지 해야 하는 총 경기수가 586경기라는 것도 쉽게 생각할 수 있다.

2개의 문제를 소개했다. 이 문제들을 소개한 이유는 문제를 같이 풀어보며 생각의 순서를 뒤바꿀 수도 있고 그렇게 하는 것이 때때로 더 쉽게 문제를 해결할 수 있다는 경험을 하기 위해서였다. 순차적으로만 생각할 수 있는 것이 아니라 순서를 바꿔서 최종적인 상황에서부터 생각을 출발할 수도 있고, 또는 관점을 달리하며 접근할 수도 있다. 이렇게 다양한 시각과 관점을 갖는 것이 생각을 더 풍부하게 하는 것이다.

어떤 대학교수가 아이들이 놀아달라고 귀찮게 굴어서 잡지에서 세계지도가 있는 페이지를 찢어서 여러 조각으로 나눠주며 퍼즐처럼 맞추게 했다고 한다. 그는 아이들이 그 퍼즐을 맞추기 위해서는 적어도 몇 시간이 걸릴 거라고 생각했다. 퍼즐을 모두 맞춰오면 맛있는 걸 사주겠다고 약속까지 했다.

그런데, 그의 생각과는 달리 아이들은 몇 분만에 퍼즐을 모두 맞춰왔다고 한다. 깜짝 놀란 대학교수는 어떻게 그것을 모두 맞췄냐고 물었다. 아이들은 웃으며 세계지도 뒷면에 있는 사람의 얼굴을 보여 줬다고 한다.

우리가 풀고 있는 복잡한 세계지도 조각의 뒷면에는 때때로 쉽게 맞출 수 있는 사람의 얼굴이 있을지도 모른다. 거꾸로 생각하며 관점을 다양하게 바꿔보는 것이 필요하다. 

글. 박종하 박종하창의력연구소 대표